Halting problem (nonfiction): Difference between revisions
No edit summary |
No edit summary |
||
| (15 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
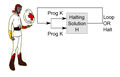
[[File:Halting_problem.svg|250px|thumb|Halting problem diagram.]]In computability theory, the '''halting problem''' is the problem of determining, from a description of an arbitrary computer program and an input, whether the program will finish running or continue to run forever. See [[Computation (nonfiction)]]. | [[File:Halting_problem.svg|250px|thumb|Halting problem diagram.]]In computability theory, the '''halting problem''' is the problem of determining, from a description of an arbitrary computer program and an input, whether the program will finish running or continue to run forever. See [[Computation (nonfiction)]]. | ||
[[Alan Turing|Alan Turing]] proved in 1936 that a general algorithm to solve the halting problem for all possible program-input pairs cannot exist. | [[Alan Turing (nonfiction)|Alan Turing]] proved in 1936 that a general algorithm to solve the halting problem for all possible program-input pairs cannot exist. | ||
A key part of the proof was a mathematical definition of a computer and program, which became known as a [[Turing machine (nonfiction)|Turing machine]]; the halting problem is undecidable over Turing machines. | A key part of the proof was a mathematical definition of a computer and program, which became known as a [[Turing machine (nonfiction)|Turing machine]]; the halting problem is undecidable over Turing machines. | ||
| Line 9: | Line 9: | ||
== In the News == | == In the News == | ||
<gallery | <gallery> | ||
File: | File:Ascleplius Myrmidon Halting Problem.jpg|link=On Halting Problems|[[On Halting Problems|Asclepius Myrmidon discovers unregistered halting problem]], predicts new class of [[crimes against mathematical constants]]. | ||
File:Forbidden_Ratio_symbol.jpg|link=Forbidden Ratio and Gnotilus (crime team)|Supervillains [[Forbidden Ratio and Gnotilus (crime team)|Forbidden Ratio and Gnotilus]] threaten to [[Weaponization (nonfiction)|weaponize]] new class of Halting problems. | |||
File:Mathematical function.svg|link=Mathematical function (nonfiction)|Law-abiding [[Mathematical function (nonfiction)|mathematical functions]] have nothing to fear from [[Crimes against mathematical constants]], say crime authorities. | |||
</gallery> | </gallery> | ||
| Line 16: | Line 18: | ||
* [[Forbidden Ratio]] | * [[Forbidden Ratio]] | ||
* [[Gnomon algorithm]] | |||
* [[Mathematics]] | |||
== Nonfiction cross-reference == | == Nonfiction cross-reference == | ||
* [[Algorithm (nonfiction)]] | |||
* [[Computation (nonfiction)]] | * [[Computation (nonfiction)]] | ||
* [[Computational complexity theory (nonfiction)]] | |||
* [[Computer algorithm (nonfiction)]] | |||
* [[Computer science (nonfiction)]] | * [[Computer science (nonfiction)]] | ||
* [[Turing machine (nonfiction)]] | |||
* [[Weapon (nonfiction)]] | |||
External links: | |||
* [https://en.wikipedia.org/wiki/Halting_problem Halting problem] @ Wikipedia | * [https://en.wikipedia.org/wiki/Halting_problem Halting problem] @ Wikipedia | ||
* [http://www.cgl.uwaterloo.ca/csk/halt/ The Halting Problem] - Craig Kaplan | |||
[[Category:Nonfiction (nonfiction)]] | [[Category:Nonfiction (nonfiction)]] | ||
[[Category:Computation (nonfiction)]] | |||
[[Category:Computer science (nonfiction)]] | |||
[[Category:Mathematics (nonfiction)]] | |||
Latest revision as of 09:23, 16 May 2018
In computability theory, the halting problem is the problem of determining, from a description of an arbitrary computer program and an input, whether the program will finish running or continue to run forever. See Computation (nonfiction).
Alan Turing proved in 1936 that a general algorithm to solve the halting problem for all possible program-input pairs cannot exist.
A key part of the proof was a mathematical definition of a computer and program, which became known as a Turing machine; the halting problem is undecidable over Turing machines.
It is one of the first examples of a decision problem.
In the News
Asclepius Myrmidon discovers unregistered halting problem, predicts new class of crimes against mathematical constants.
Supervillains Forbidden Ratio and Gnotilus threaten to weaponize new class of Halting problems.
Law-abiding mathematical functions have nothing to fear from Crimes against mathematical constants, say crime authorities.
Fiction cross-reference
Nonfiction cross-reference
- Algorithm (nonfiction)
- Computation (nonfiction)
- Computational complexity theory (nonfiction)
- Computer algorithm (nonfiction)
- Computer science (nonfiction)
- Turing machine (nonfiction)
- Weapon (nonfiction)
External links:
- Halting problem @ Wikipedia
- The Halting Problem - Craig Kaplan