Rational number (nonfiction)

Diagram to demonstrate the number systems ℝ, ℚ, ℤ and ℕ as sub-sets of each other. Real numbers (R) include the rational numbers (Q), which include the integers (Z), which include the natural numbers (N).

In mathematics, a rational number is any number that can be expressed as the quotient or fraction p/q of two integers, a numerator p and a non-zero denominator q. Since q may be equal to 1, every integer is a rational number.

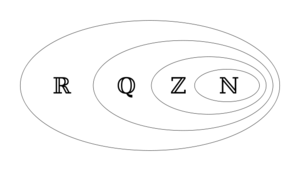
The set of all rational numbers, often referred to as "the rationals", the field of rationals or the field of rational numbers is usually denoted by a boldface Q, blackboard bold Q, Unicode ℚ); it was thus denoted in 1895 by Giuseppe Peano after quoziente, Italian for "quotient".

The decimal expansion of a rational number always either terminates after a finite number of digits or begins to repeat the same finite sequence of digits over and over. Moreover, any repeating or terminating decimal represents a rational number. These statements hold true not just for base 10, but also for any other integer base (e.g. binary, hexadecimal).

A real number that is not rational is called irrational. Irrational numbers include √2, π, e, and the Golden ratio φ. Since the set of rational numbers is countable, and the set of real numbers is uncountable, almost all real numbers are irrational.

Rational numbers can be formally defined as equivalence classes of pairs of integers (p, q) such that q ≠ 0, for the equivalence relation defined by (p1,q1) ~ (p2,q2) if, and only if, p1q2 = p2q1.

The rational numbers together with addition and multiplication form a field which contains the integers and is contained in any field containing the integers.

Finite extensions of Q are called algebraic number fields, and the algebraic closure of Q is the field of algebraic numbers.

In mathematical analysis, the rational numbers form a dense subset of the real numbers. The real numbers can be constructed from the rational numbers by completion, using Cauchy sequences, Dedekind cuts, or infinite decimals.

In the News

• 

  New study of integers indicates that they "may be vulnerable to crimes against mathematical constants."

• 

  Diagram of hand holding up two fingers is "honored to represent the entire class of natural numbers, within the larger set of rational numbers."

Nonfiction cross-reference

• Integer (nonfiction)
• Irrational number (nonfiction)

External links:

• Rational number @ Wikipedia