Polyhedron (nonfiction): Difference between revisions
(Created page with "In elementary geometry, a '''polyhedron''' (plural '''polyhedra''' or '''polyhedrons''') is a solid in three dimensions with flat polygonal faces, st...") |
|||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
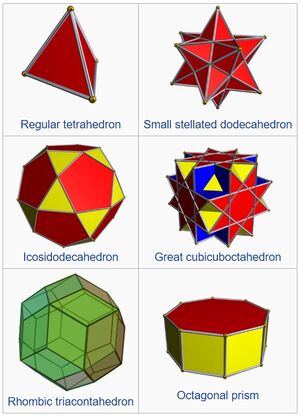
In elementary [[Geometry (nonfiction)|geometry]], a '''polyhedron''' (plural '''polyhedra''' or '''polyhedrons''') is a solid in three dimensions with flat polygonal faces, straight edges and sharp corners or vertices. | [[File:Polyhedra.jpg|thumb|Six different types of polyhedra.]]In elementary [[Geometry (nonfiction)|geometry]], a '''polyhedron''' (plural '''polyhedra''' or '''polyhedrons''') is a solid in three dimensions with flat polygonal faces, straight edges and sharp corners or vertices. | ||
The word polyhedron comes from the Classical Greek πολύεδρον, as ''poly''- (stem of πολύς, "many") + -''hedron'' (form of ἕδρα, "base" or "seat"). | The word polyhedron comes from the Classical Greek πολύεδρον, as ''poly''- (stem of πολύς, "many") + -''hedron'' (form of ἕδρα, "base" or "seat"). | ||
| Line 12: | Line 12: | ||
<gallery mode="traditional"> | <gallery mode="traditional"> | ||
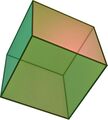
File:Hexahedron.jpg|link=Cube (nonfiction)|[[Cube (nonfiction)|Cube]] says it is "satisfied with six faces", is not jealous of other polyhedra. | |||
</gallery> | </gallery> | ||
Latest revision as of 12:16, 20 November 2016
In elementary geometry, a polyhedron (plural polyhedra or polyhedrons) is a solid in three dimensions with flat polygonal faces, straight edges and sharp corners or vertices.
The word polyhedron comes from the Classical Greek πολύεδρον, as poly- (stem of πολύς, "many") + -hedron (form of ἕδρα, "base" or "seat").
Cubes and pyramids are examples of polyhedra.
A polyhedron is said to be convex if its surface (comprising its faces, edges and vertices) does not intersect itself and the line segment joining any two points of the polyhedron is contained in the interior or surface.
A polyhedron is a 3-dimensional example of the more general polytope in any number of dimensions.
In the News
Cube says it is "satisfied with six faces", is not jealous of other polyhedra.
Fiction cross-reference
Nonfiction cross-reference
External links:
- Polyhedron @ Wikipedia