Binomial theorem (nonfiction): Difference between revisions
No edit summary |
No edit summary |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
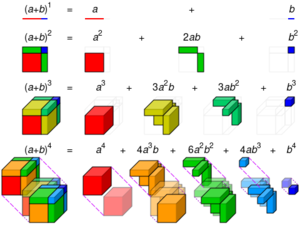
In [[Elementary algebra (nonfiction)|elementary algebra]], the '''binomial theorem''' (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the polynomial (x + y)n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with b + c = n, and the coefficient a of each term is a specific positive integer depending on n and b. | [[File:Binomial theorem visualization.svg|thumb|Visualization of binomial expansion up to the 4th power.]]In [[Elementary algebra (nonfiction)|elementary algebra]], the '''binomial theorem''' (or binomial expansion) describes the algebraic expansion of [[Exponentiation (nonfiction)|powers]] of a [[Binomial (polynomial) (nonfiction)|binomial]]. According to the theorem, it is possible to expand the polynomial (x + y)n into a [[Summation (nonfiction)|sum]] involving terms of the form axbyc, where the exponents b and c are [[Natural number (nonfiction)|nonnegative integers]] with b + c = n, and the [[Coefficient (nonfiction)|coefficient]] a of each term is a specific positive integer depending on n and b. | ||
The coefficient a in the term of axbyc is known as the [[Binomial coefficient (nonfiction)|binomial coefficient]] ... TO_DO .... | |||
== History == | |||
Special cases of the binomial theorem were known since at least the 4th century BC when [[Greek mathematics (nonfiction)|Greek mathematician]] [[Euclid (nonfiction)|Euclid]] mentioned the special case of the binomial theorem for exponent 2. There is evidence that the binomial theorem for cubes was known by the 6th century AD in India. | |||
Binomial coefficients, as combinatorial quantities expressing the number of ways of selecting k objects out of n without replacement, were of interest to ancient Indian mathematicians. The earliest known reference to this combinatorial problem is the ''[[Chandaḥśāstra (nonfiction)|Chandaḥśāstra]]'' by the Indian lyricist [[Pingala (nonfiction)|Pingala]] (c. 200 BC), which contains a method for its solution. The commentator [[Halayudha (nonfiction)|Halayudha]] from the 10th century AD explains this method using what is now known as [[Pascal's triangle (nonfiction)|Pascal's triangle]]. By the 6th century AD, the Indian mathematicians probably knew how to express this as a quotient TO_DO, and a clear statement of this rule can be found in the 12th century text ''[[Lilavati (nonfiction)|Lilavati]]'' by [[Bhāskara II (nonfiction)|Bhāskara II]]. | |||
The first formulation of the binomial theorem and the table of binomial coefficients, to our knowledge, can be found in a work by [[Al-Karaji (nonfiction)|Al-Karaji]], quoted by [[Al-Samawal al-Maghribi (nonfiction)|Al-Samaw'al]] in his "al-Bahir". Al-Karaji described the triangular pattern of the binomial coefficients and also provided a mathematical proof of both the binomial theorem and Pascal's triangle, using an early form of [[Mathematical induction (nonfiction)|mathematical induction]]. The Persian poet and mathematician [[Omar Khayyam (nonfiction)|Omar Khayyam]] was probably familiar with the formula to higher orders, although many of his mathematical works are lost. The binomial expansions of small degrees were known in the 13th century mathematical works of [[Yang Hui (nonfiction)|Yang Hui]] and also [[Zhu Shijie (nonfiction)|Chu Shih-Chieh]]. Yang Hui attributes the method to a much earlier 11th century text of [[Jia Xian (nonfiction)|Jia Xian]]; these writings are now also lost. | |||
In 1544, [[Michael Stifel (nonfiction)|Michael Stifel]] introduced the term "binomial coefficient" and showed how to use them to express TO_DO .... [[Blaise Pascal (nonfiction)|Blaise Pascal]] studied the eponymous triangle comprehensively in the treatise ''[[Traité du triangle arithmétique (nonfiction)|Traité du triangle arithmétique]]'' (1665). However, the pattern of numbers was already known to the European mathematicians of the late Renaissance, including Stifel, [[Niccolò Fontana Tartaglia (nonfiction)|Niccolò Fontana Tartaglia]], and [[Simon Stevin (nonfiction)|Simon Stevin]]. | |||
[[Isaac Newton (nonfiction)|Isaac Newton]] is generally credited with the generalized binomial theorem, valid for any rational exponent. | |||
== In the News == | |||
<gallery> | |||
</gallery> | |||
== Fiction cross-reference == | |||
* [[Crimes against mathematical constants]] | |||
* [[Gnomon algorithm]] | |||
* [[Gnomon Chronicles]] | |||
* [[Mathematics]] | |||
== Nonfiction cross-reference == | |||
* [[Binomial (polynomial) (nonfiction)]] - a [[Polynomial (nonfiction)|polynomial]] that is the sum of two terms, each of which is a monomial. It is the simplest kind of polynomial after the monomials. | |||
* [[Binomial coefficient (nonfiction)]] | |||
* [[Elementary algebra (nonfiction)]] | |||
* [[Exponentiation (nonfiction)]] | |||
* [[Mathematics (nonfiction)]] | |||
* [[Polynomial (nonfiction)]] | |||
== External links == | |||
* [https://en.wikipedia.org/wiki/Binomial_theorem Binomial theorem] @ Wikipedia | |||
[[Category:Nonfiction (nonfiction)]] | |||
[[Category:Mathematics (nonfiction)]] | |||
[[Category:Math needed (nonfiction)]] | |||
Latest revision as of 06:54, 19 April 2020
In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the polynomial (x + y)n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with b + c = n, and the coefficient a of each term is a specific positive integer depending on n and b.
The coefficient a in the term of axbyc is known as the binomial coefficient ... TO_DO ....
History
Special cases of the binomial theorem were known since at least the 4th century BC when Greek mathematician Euclid mentioned the special case of the binomial theorem for exponent 2. There is evidence that the binomial theorem for cubes was known by the 6th century AD in India.
Binomial coefficients, as combinatorial quantities expressing the number of ways of selecting k objects out of n without replacement, were of interest to ancient Indian mathematicians. The earliest known reference to this combinatorial problem is the Chandaḥśāstra by the Indian lyricist Pingala (c. 200 BC), which contains a method for its solution. The commentator Halayudha from the 10th century AD explains this method using what is now known as Pascal's triangle. By the 6th century AD, the Indian mathematicians probably knew how to express this as a quotient TO_DO, and a clear statement of this rule can be found in the 12th century text Lilavati by Bhāskara II.
The first formulation of the binomial theorem and the table of binomial coefficients, to our knowledge, can be found in a work by Al-Karaji, quoted by Al-Samaw'al in his "al-Bahir". Al-Karaji described the triangular pattern of the binomial coefficients and also provided a mathematical proof of both the binomial theorem and Pascal's triangle, using an early form of mathematical induction. The Persian poet and mathematician Omar Khayyam was probably familiar with the formula to higher orders, although many of his mathematical works are lost. The binomial expansions of small degrees were known in the 13th century mathematical works of Yang Hui and also Chu Shih-Chieh. Yang Hui attributes the method to a much earlier 11th century text of Jia Xian; these writings are now also lost.
In 1544, Michael Stifel introduced the term "binomial coefficient" and showed how to use them to express TO_DO .... Blaise Pascal studied the eponymous triangle comprehensively in the treatise Traité du triangle arithmétique (1665). However, the pattern of numbers was already known to the European mathematicians of the late Renaissance, including Stifel, Niccolò Fontana Tartaglia, and Simon Stevin.
Isaac Newton is generally credited with the generalized binomial theorem, valid for any rational exponent.
In the News
Fiction cross-reference
Nonfiction cross-reference
- Binomial (polynomial) (nonfiction) - a polynomial that is the sum of two terms, each of which is a monomial. It is the simplest kind of polynomial after the monomials.
- Binomial coefficient (nonfiction)
- Elementary algebra (nonfiction)
- Exponentiation (nonfiction)
- Mathematics (nonfiction)
- Polynomial (nonfiction)
External links
- Binomial theorem @ Wikipedia