Coxeter's loxodromic sequence of tangent circles (nonfiction): Difference between revisions

From Gnomon Chronicles
Jump to navigation Jump to search
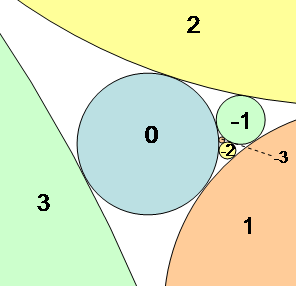
(Created page with "[[|thumb|Blue circle 0 is tangent to circles 1, 2 and 3, as well as to preceding circles −1, −2 and −3.]]In geometry, Coxeter's loxodromic sequence of tangent circles is...")
 
No edit summary
Line 1: Line 1:
[[|thumb|Blue circle 0 is tangent to circles 1, 2 and 3, as well as to preceding circles −1, −2 and −3.]]In geometry, Coxeter's loxodromic sequence of tangent circles is an infinite sequence of circles arranged so that any four consecutive circles in the sequence are pairwise mutually tangent. This means that each circle in the sequence is tangent to the three circles that precede it and also to the three circles that follow it.
[[File:Coxeter_circles.png|thumb|Blue circle 0 is tangent to circles 1, 2 and 3, as well as to preceding circles −1, −2 and −3.]]In geometry, Coxeter's loxodromic sequence of tangent circles is an infinite sequence of circles arranged so that any four consecutive circles in the sequence are pairwise mutually tangent. This means that each circle in the sequence is tangent to the three circles that precede it and also to the three circles that follow it.


== In the News ==
== In the News ==

Revision as of 17:55, 28 March 2018

Blue circle 0 is tangent to circles 1, 2 and 3, as well as to preceding circles −1, −2 and −3.

In geometry, Coxeter's loxodromic sequence of tangent circles is an infinite sequence of circles arranged so that any four consecutive circles in the sequence are pairwise mutually tangent. This means that each circle in the sequence is tangent to the three circles that precede it and also to the three circles that follow it.

In the News

Fiction cross-reference

Nonfiction cross-reference

External links:

  • [] @ Wikipedia

Attribution:

Retrieved from "https://gnomonchronicles.com/w/index.php?title=Coxeter%27s_loxodromic_sequence_of_tangent_circles_(nonfiction)&oldid=29894"